Verwendung neuronaler Netze zur Erkennung handgeschriebener Ziffern

Sieh Dir die folgenden handgeschriebenen Ziffern an:

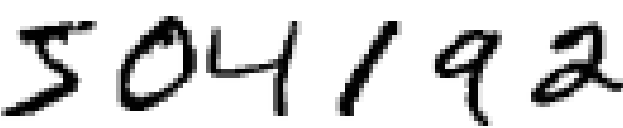
Die meisten Menschen erkennen hier mühelos die Ziffern 504192. Die Leichtigkeit, mit der ihnen das gelingt, ist trügerisch. Handgeschriebene Ziffern zu erkennen, ist nicht einfach. Wir Menschen sind vielmehr erstaunlich gut darin, in dem, was unsere Augen sehen, einen Sinn zu erkennen. Deshalb wertschätzen wir gewöhnlich nicht, wie schwierig die Herausforderungen sind, die unser visuelles System meistert.

In jeder Hemisphäre unseres Gehirns haben wir Menschen einen primären visuellen Kortex (V1), der ca. 140 Millionen Neuronen enthält, mit zig Milliarden Verbindungen zwischen ihnen. Und dennoch umfasst das menschliche Sehvermögen nicht nur V1, sondern eine ganze Serie von visuellen Gehirnrinden (V2, V3, V4, V5), die zunehmend komplexere Bildverarbeitung betreiben. Wir haben in unserem Kopf einen Supercomputer, der durch die Evolution über hunderte von Millionen Jahren darauf abgestimmt wurde, die visuelle Welt zu verstehen.

Wie schwierig die visuelle Mustererkennung ist, wird offensichtlich, wenn man versucht, ein Computerprogramm zur Erkennung von handgeschriebenen Ziffern zu schreiben. Was einfach wirkt, wenn wir Menschen es selbst tun, wird plötzlich extrem schwierig, wenn wir den Computer dazu anweisen wollen. Es stellt sich heraus, dass es nicht so einfach ist, unsere Intuitionen, wie wir Formen, Umrisse, Konturen erkennen ("eine 9 hat oben eine Schlaufe und rechts unten einen senkrechten Strich") in Algorithmen auszudrücken. Wenn man versucht, präzise Regeln zu formulieren, verliert man sich schnell in einem Sumpf von Ausnahmen und Spezialfällen. Dieser Weg erscheint aussichtslos.

Neuronale Netze nähern sich dem Problem auf andere Art. Die Idee ist, eine große Anzahl handgeschriebener Ziffern als Trainingsbeispiele heranzuziehen und dann ein System zu entwickeln, welches selbst lernt, aus diesen Beispieldaten Regeln zur Ziffernerkennung abzuleiten.

Ich zeige oben nur 100 Trainingsziffern. Durch Erhöhung der Anzahl der Trainingsbeispiele kann das Netz mehr über Handschriften lernen und seine Genauigkeit verbessern. Mit Tausenden, Millionen oder Milliarden Trainingsbeispielen können wir vielleicht einen besseren Handschriften-Erkenner erstellen.

In diesem Kapitel werden wir ein Programm schreiben, das ein neuronales Netz implementiert, das lernt handgeschriebene Ziffern zu erkennen. Das Programm ist nur 74 Zeilen lang und nutzt keine spezielle Bibliothek für neuronale Netze. Aber dieses kurze Programm kann Ziffern ohne menschliches Zutun mit einer Genauigkeit von mehr als 96 Prozent erkennen. Später werden wir Ideen entwickeln, welche die Genauigkeit auf über 99 Prozent steigern können. Tatsächlich sind die besten kommerziellen neuronalen Netze heute so gut, dass sie von Banken verwendet werden, um Schecks zu bearbeiten und von der Post, um Adressen zu erkennen.

Wir konzentrieren uns auf die Erkennung von Handschriften, weil dies ein ausgezeichnetes Musterproblem für das Lernen über neuronale Netze ist. Es ist fordernd, aber nicht so schwierig, dass es extrem komplizierte Lösungen oder besonders große Rechenleistung erfordern würde. Außerdem eignet es sich, um hieran fortgeschrittene Techniken wie Deep Learning zu entwickeln. Später im Buch werden wir besprechen, wie wir diese Ideen auf andere Probleme der Bild- und Spracherkennung sowie der Verarbeitung natürlicher Sprache und weiterer Gebiete anwenden können.

Wenn der Zweck des Kapitels nur wäre, ein Programm zur Erkennung handgeschriebener Ziffern zu schreiben, dann wäre es natürlich deutlich kürzer. Aber wir werden nebenbei viele Schlüsselideen über neuronale Netze entwickeln. Das schließt zwei wichtiger Arten von künstlichen Neuronen (Perzpetron und Sigmoid-Neuron) und den Standard-Lernalgorithmus für neuronale Netze ein, der als stochastischer Gradientenabstieg (SGD) bekannt ist.

Durchgängig konzentriere ich mich darauf zu erklären, warum alles so gemacht wird, wie es gemacht wird und darauf, Dein Gespür für neuronale Netze aufzubauen. Das erfordert ausführlichere Besprechungen als wenn ich nur die grundlegenden Funktionsweisen darstellen würde. Aber es ist Dein tieferes Verständnis wert. Als Lohn werden wir am Ende des Kapitels in der Lage sein, zu verstehen, was Deep Learning ist und warum es wichtig ist.

Das Perzeptron

Was ist ein neuronales Netz? Um das zu beantworten, erkläre ich zunächst ein einzelnes Neuron. Und zwar das sogenannte Perzeptron.

Das Perzeptron ist eine Art von künstlichem Neuron. Es wurde in den 50er und 60er Jahren durch den Wissenschaftler Frank Rosenblatt entwickelt, der durch frühere Arbeiten von Warren McCulloch und Walter Pitts inspiriert worden war. Heute werden üblicherweise andere Modelle künstlicher Neuronen verwendet. In diesem Buch und in vielen modernen Arbeiten über neuronale Netze wird überwiegend das Modell des Sigmoid-Neurons verwendet. Zu den (etwas komplexeren) Sigmoid-Neuronen kommen wir gleich. Aber um zu verstehen, warum Sigmoid-Neuronen so definiert sind, wie sie sind, lohnt es sich, dass wir uns etwas Zeit nehmen, zunächst Perzeptronen zu verstehen.

Wie funktioniert ein Perzeptron?

Ein Perzeptron empfängt mehrere binäre Eingabewerte (\(x_1, x_2, \ldots\)), also jeweils eine \(0\) oder \(1\), und erstellt daraus einen einzigen binären Ausgabewert:

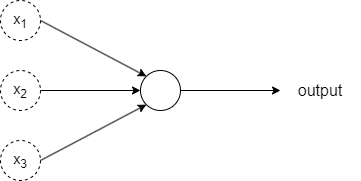
In dem oben gezeigten Beispiel hat das Perzeptron drei Eingabewerte (\(x_1, x_2, x_3\)). Generell kann ein Perzeptron auch mehr oder weniger Eingabewerte haben.

Zur Berechnung des Ausgabewerts schlug Rosenblatt eine einfache Regel vor. Er führte Gewichte (\(w_1, w_2, \ldots\)) und einen Schwellwert (\(threshold\)) als Parameter des Neurons ein. Beides sind reelle Zahlen. Die Gewichte geben die Wichtigkeit der jeweiligen Eingabewerte für den Ausgabewert des Neurons an. Der Ausgabewert des Neurons (\(0\) oder \(1\)) wird dadurch bestimmt, ob die gewichtete Summe der Eingabewerte $\sum_j w_j x_j$ kleiner oder größer als der Schwellwert des Neurons ist. Um es algebraisch präziser auszudrücken:

\begin{eqnarray} \mbox{output} & = & \left\{ \begin{array}{ll} 0 & \mbox{if } \sum_j w_j x_j \leq \mbox{ threshold} \\ 1 & \mbox{if } \sum_j w_j x_j > \mbox{ threshold} \end{array} \right. \end{eqnarray}

Das ist schon alles, was es zur Funktionsweise eines Perzeptrons zu sagen gibt. Das ist das grundlegende mathematische Modell. Du kannst Dir das Perzeptron also als eine Apparatur vorstellen, die Entscheidungen auf Basis von gewichteten Einflussgrößen trifft.

Ich gebe Dir ein Beispiel:

Angenommen Du erfährst, dass es noch einige restliche Eintrittskarten für ein Freiluftkonzert der Elektropop-Band Kraftwerk am kommenden Wochenende in Deiner Nähe gibt. Du magst Kraftwerk und möchtest die Entscheidung treffen, ob Du eine Eintrittskarte kaufst. Du könntest Deine Entscheidung von drei Faktoren abhängig machen:

• Ist die Wettervorhersage gut?
• Kommt Deine Freundin/Freund mit?
• Ist der Veranstaltungsort gut mit öffentlichen Verkehrsmitteln zu erreichen? (Du hast kein Auto)

Wir können ein Perzeptron verwenden, um die Entscheidungsfindung zu modellieren. Die drei Faktoren können wir durch binäre Variablen $x_1, x_2$, and $x_3$ repräsentieren. Wir können $x_1 = 1$ setzen, wenn gutes Wetter vorhergesagt wird und $x_1 = 0$ wenn Regen vorhergesagt wird. Wir können $x_2 = 1$ setzen, wenn Deine Freundin/Freund mitkommen würde, und $x_2 = 0$ wenn nicht. Und wir können $x_3 =1$ setzen, wenn der Veranstaltungsort gut mit öffentlichen Verkehrsmitteln erreichbar ist und $x_3 = 0$ wenn nicht.

Nehmen wir an, dass Du Kraftwerk so sehr magst, dass Du auch dann gerne das Konzert besuchen würdest, wenn Dein Freund/Freundin nicht mitkommen würde und der Veranstaltungsort nur umständlich mit öffentlichen Verkehrsmitteln erreichbar ist. Aber vielleicht verabscheust Du schlechtes Wetter so sehr, dass Du das Konzert bei Regen nicht besuchen würdest.

Um Deine Präferenzen (die Bedeutung der Faktoren) zu modellieren, könntest Du ein Gewicht $w_1 = 6$ für das Wetter, und $w_2 = 2$ und $w_3 = 2$ für die beiden anderen Faktoren wählen. Der größere Wert für $w_1$ zeigt an, dass der Faktor Wetter für Dich deutlich wichtiger ist als die beiden anderen Faktoren. Nehmen wir schließlich noch an, dass Du einen Schwellwert von $5$ für das Perzeptron wählst.

Mit dieser Wahl der Parameter implementiert das Perzeptron das gewünschte Entscheidungsfindungsmodell. Das Perzeptron gibt $1$ aus, wenn das Wetter gut ist und $0$, wenn das Wetter schlecht ist. Ob Deine Freundin/Freund mitkommt oder nicht, macht keinen Unterschied. Genauso macht es keinen Unterschied, ob der Veranstaltungsort gut oder schlecht per ÖPNV erreichbar ist.

Indem wir die Gewichte und den Schwellwert verändern, können wir andere Entscheidungsfindungsmodelle modellieren. Falls wir beispielsweise als Schwellwert $3$ wählen, würde das Perzeptron entscheiden, dass Du ein Konzertticket kaufen solltest, wenn entweder das Wetter gut ist oder sowohl Deine Freundin/Freund mitkommen würde und der Veranstaltungsort gut per ÖPNV erreichbar ist. Das Senken des Schwellwerts bedeutet, dass Du eher bereit bist, eine Eintrittskarte zu kaufen.

Netzwerk von Perzeptronen

Das Perzeptron ist offensichtlich kein vollständiges Modell menschlicher Entscheidungsfindung! Aber das obige Beispiel veranschaulicht wie ein Perzeptron verschiedene Einflussfaktoren abwägen kann, um zu einer Entscheidung zu kommen. Es sollte plausibel erscheinen, dass ein komplexes Netzwerk von Perzeptronen ziemlich anspruchsvolle Entscheidungen treffen kann:

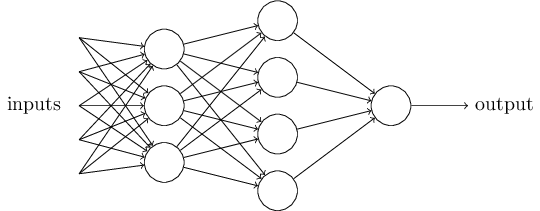
In obigem Netzwerk trifft die erste Schicht von Perzeptronen drei einfache Entscheidungen. Was ist mit den Perzeptronen in der zweiten Schicht? Jedes dieser Perzeptronen trifft eine Entscheidung durch Abwägung der Ergebnisse aus der ersten Entscheidungsfindungs-Schicht. Auf diese Weise kann ein Perzeptron der zweiten Schicht eine Entscheidung auf einem komplexeren und abstrakteren Level treffen als jene der ersten Schicht. Und noch komplexere Entscheidungen können in der dritten Schicht getroffen werden. Auf diese Weise kann ein mehrschichtiges Perzeptronen-Netzwerk ausgefeilte Entscheidungen treffen.

Das Perzeptron hat nur einen einzigen Ausgabewert. Die vielen Pfeile, die von einem Perzeptron ausgehen, sind nur dazu eingezeichnet, um anzuzeigen, dass der Output eines Perzeptrons als Input für mehrere andere Perzeptrone genutzt wird.

Lass uns die Beschreibung des Perzeptrons vereinfachen. Die Bedingung $\sum_j w_j x_j > \mbox{threshold}$ ist umständlich. Wir können zwei Änderungen an der Notation vornehmen, um sie zu vereinfachen - und auch um sie für die anderen Neuronen vorzubereiten? Die erste Änderung ist $\sum_j w_j x_j$ als Skalarprodukt ("dot product"), $w \cdot x \equiv \sum_j w_j x_j$, zu schreiben, wobei $w$ und $x$ Vektoren sind, deren Bausteine die Gewichte und Eingabewerte sind. The second change is to move the threshold to the other side of the inequality, and to replace it by what's known as the perceptron's bias (Verzerrung), $b \equiv -\mbox{threshold}$. Using the bias instead of the threshold, the perceptron rule can be rewritten:

\begin{eqnarray} \mbox{output} = \left\{ \begin{array}{ll} 0 & \mbox{if } w\cdot x + b \leq 0 \\ 1 & \mbox{if } w\cdot x + b > 0 \end{array} \right. \end{eqnarray}

Diese Funktion ("Für jeden Eingabewert größer als 0 ist der Ausgabewert 1 und sonst 0") entspricht fast genau der Heaviside-Funktion, die ich gleich vorstellen werde. Sie unterscheidet sich von ihr nur für den Eingabewert 0. Für diesen Wert gibt die Heaviside-Funktion nämlich den Wert 1 zurück.

Der folgende Graph der Heaviside-Funktion zeigt anschaulich, welchen Ausgabewert die Funktion für jeden Eingabewert zurückgibt:

Perzeptronen unterscheiden sich von komplexeren Neuronen im Kern nur durch einen Umstand:

• Sie nutzen als Aktivierungsfunktion die Schwellenwertfunktion (Heaviside-Funktion), die als Ausgabewert nur entweder eine 0 oder eine 1 liefert.
• Da in einem neuronalen Netz mehrere Perzeptronen miteinander verbunden sind, ergibt sich daraus, dass sie als Input binäre Werte erwarten.

Lernalgorithmen klingen fantastisch. Aber wie können wir solche Algorithmen für ein neuronales Netz entwickeln? Nehmen wir an, wir haben ein Netzwerk aus Perzeptronen, das wir dazu verwenden möchten, um zu lernen, ein Problem zu lösen.

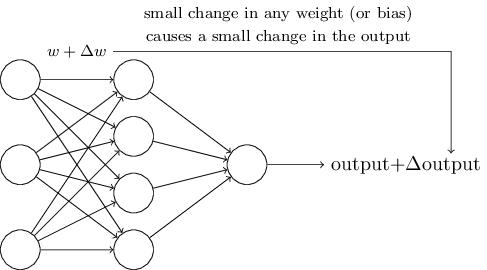
Wenn es zutreffend wäre, dass eine kleine Änderung eines Gewichts (oder Biases) nur eine kleine Veränderung beim Output verursachen würde, dann könnten wir diese Tatsache nutzen, um die Gewichte und Biase zu ändern, um unser neuronales Netz dazu zu bringen, sich mehr so zu verhalten wie wir es wollen. Nehmen wir beispielsweise an, dass das Netz ein Bild einer Ziffer als "8" klassifiziert, während es eigentlich als "9" klassifiziert werden sollte. Wir könnten herausfinden, wie wir eine kleine Änderung bei den Gewichten und Biasen vornehmen, welche das Netzwerk näher dahin bringt, dass Bild als "9" zu klassifizieren. Und dann wiederholen wir das, ändern die Gewichte und Biase immer wieder um immer bessere Ergebnisse zu erzielen. Das Netzwerk würde lernen.

Das Problem ist, dass dies nicht der Fall ist, wenn das Netzwerk aus Perzeptronen besteht. Tatsächlich können kleine Änderungen in den Gewichten und Biasen eines einzelnen Perzeptrons dazu führen, dessen Output komplett umzukehren, etwa von 0 zu 1. Dieser Flip kann dann das Verhalten des restlichen Netzes komplett in einer komplizierten Weise ändern.

...

Das Sigmoid-Neuron

Wir können das Problem überwinden, indem wir eine neue Art Neuron einführen, welches Sigmoid-Neuron genannt wird. Sigmoid-Neuronen sind gegenüber den Perzeptronen dahingehend geändert, dass kleine Änderungen ihrer Gewichte und Biase nur kleine Änderungen ihres Outputs bewirken. Diese Eigenschaft ermöglicht es einem Netzwerk aus Sigmoid-Neuronen zu lernen.

...

Die Sigmoidfunktion transformiert wie die Schwellenwertfunktion jeden reellen Wert in einen Bereich zwischen 0 und 1. Ihre S-Form ist eine geglättete Version der Schwellenwertfunktion:

Die Architektur neuronaler Netze

...

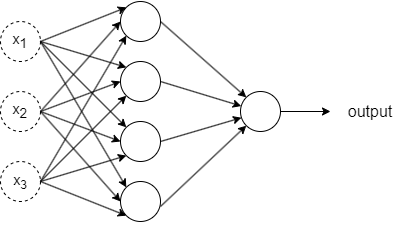
Ein einfaches Netzwerk zur Klassifizierung handgeschriebener Ziffern

...

Lernen mittels Gradientenabstieg

...

Wir implementieren unser Netzwerk zur Ziffernklassifizierung

Wir werden nun ein nur 74 Zeilen kurzes Python-Programm schreiben, das mittels stochastischem Gradientenabstieg lernt, handgeschriebene Ziffern zu erkennen. Wir verwenden dazu den MNIST-Datensatz.

...

Code wird überwiegend in englischer Sprache verfasst und ich werde hier in den Code-Blöcken englische Ausdrücke verwenden.

import numpy as np

class Network(object):

    def __init__(self, sizes):
        """The list ``sizes`` contains the number of neurons in the
        respective layers of the network.  For example, if the list
        was [2, 3, 1] then it would be a three-layer network, with the
        first layer containing 2 neurons, the second layer 3 neurons,
        and the third layer 1 neuron.  The biases and weights for the
        network are initialized randomly, using a Gaussian
        distribution with mean 0, and variance 1.  Note that the first
        layer is assumed to be an input layer, and by convention we
        won't set any biases for those neurons, since biases are only
        ever used in computing the outputs from later layers."""

        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
        self.weights = [np.random.randn(y, x)
                        for x, y in zip(sizes[:-1], sizes[1:])]

Hin zu Deep Learning

...